कर्तन छोर की ज्यामिति

 

 

 

यंत्रण प्रक्रिया में टूल के कर्तन छोर (कटिंग एज) की ज्यामिति का महत्व बहुत ज्यादा है। इस लेख में हम उसके बारे में जानकारी हासिल करेंगे।

किसी भी इन्सर्ट के काम की जांच करते समय आगे दी गई बातों को ध्यान में रखना जरूरी होता है।

1. इस्तेमाल किए हुए कार्बाइड की श्रेणी (ग्रेड) से इन्सर्ट की विशेषताएं निश्चित की जाती हैं। कार्यवस्तु के मटीरीयल के अनुसार ग्राहक द्वारा कार्बाइड की श्रेणी को निश्चित करना अपेक्षित होता है। इन दोनों में साझा घटक होता है यंत्रण की गति (कटिंग स्पीड)। चुनाव कुछ इस तरीके में करना पड़ता है कि यंत्रण की गति और कार्बाइड की श्रेणी, दोनों घटक एक दूसरे के पूरक बने।

2. इन्सर्ट की विशेषताएं, उसकी ज्यामिति पर बड़े पैमाने में निर्भर करती हैं। कार्यवस्तु पर किस तरह का यंत्रण करना है, उसी के अनुसार इन्सर्ट की ज्यामिति चुनना जरूरी होता है। उदाहरण के लिए रफिंग या फिनिशिंग ऑपरेशन, इन दोनों में से कौनसा काम करना है उसी के अनुसार इन्सर्ट की ज्यामिति का चुनाव करना पड़ता है। इसमें साझा घटक है यंत्रण करते समय की ज्यामितीय कर्तन (कटिंग) स्थिति, अर्थात सरकन गति (फीड) और काट की गहराई (डेप्थ ऑफ कट) ।

इस लेख में हम काट की गहराई, सरकने की गति और यंत्रण के प्रकार इन घटकों के आधार पर कर्तन छोरों की ज्यामिति के बारे में अभ्यास करेंगे।

 

 

'सिंटर्ड इन' इन्सर्ट की ज्यामिति के मुख्य रूप से दो प्रकार होते हैं।

1. माइक्रो जिऑमिट्री या माइक्रो शार्प जिऑमिट्री : इस तरह की ज्यामिति कर्तन छोर से काफी जुड़ी हुई रहती है। ऐसी ज्यामिति के कारण यंत्रण के दौरान जिस पल चिप तैयार होती हैं, उसी समय उन्हें मोड़ा (बेंड किया) जाता है, काटा जाता है और निकाल दिया जाता है। इस प्रकार की ज्यामिति को F नाम से दर्शाया जाता है। F प्रकार की विशेष ज्यामिति के कारण छोटी चिप तैयार होती हैं। ऐसी कर्तन छोर की यांत्रिकी ताकत (मेकेैनिकल स्ट्रेंग्थ) कम होती है। सारा ध्यान कर्तन छोर पर केंद्रित होने के कारण भुरभुरापन बढ़ जाता है। इसलिए काट की गहराई और सरकने की गति को कम रखना पड़ता है।

2. रफिंग जिऑमिट्री: इस ज्यामिति को R नाम से जाना जाता है। इस तरह की ज्यामिति से लाभ यह है कि, कर्तन छोर मजबूत होते हैं। लेकिन R प्रकार की ज्यामिति से नुकसान यह रहता है कि, चिप बनते समय उन्हें अधिक आजादी मिलती है और लंबी चिप तैयार होती हैं।

3. M जिऑमिट्री: F और R ज्यामिति के संयोजन (कॉम्बिनेशन) से जो तीसरी ज्यामिति तैयार होती है उसे हम M ज्यामिति के नाम से जानते हैं। उदाहरण के लिए, नई MF5 ज्यामिति। इस ज्यामिति के कारण अधिकतम यांत्रिकी ताकत मिलती है और चिप को अधिक क्षमता से काटा जाता है। कटिंग टूल क्षेत्र में इस तरह की ज्यामिति अत्यंत आकर्षक साबित होती है।

किसी भी प्रकार की ज्यामिति का इन्सर्ट हो, उसके द्वारा हम अधिकतम क्षमता से यंत्रण कर सकते हैं। यह नतीजा पाने के लिए हमें यंत्रण की स्थिति में, काट की गहराई और सरकन गति से संबंधित कुछ बुनियादी नियमों का ध्यान रखना पड़ेगा।

 

 

काट की गहराई, इन्सर्ट की नाक की त्रिज्या (नोज रेडियस) से कम नहीं होनी चाहिए। जैसे, अगर इन्सर्ट के नाक की त्रिज्या 0.8 मिमी. हो, तो काट की गहराई सामान्यतः 0.8 मिमी. होनी चाहिए। लेकिन फिनिशिंग ऑपरेशन में कभी कभी मर्यादाएं आती हैं। हमें ध्यान रखना पड़ता है कि फिनिशिंग के दौरान इस मर्यादा के नीचे जाने पर लंबी चिप तैयार होती हैं।

चुनी हुई काट की गहराई बहुत ज्यादा भी नहीं हो सकती क्योंकि उसके कारण इन्सर्ट पर अतिरिक्त यांत्रिकी भार पड़ता है और इन्सर्ट टूटने की संभावना होती है। काट की गहराई, कर्तन छोर की उचित लंबाई के ¾ (यानि 75%) से ज्यादा नहीं होनी चाहिए। V प्रकार के नाजुक इन्सर्ट के लिए हमें काट की गहराई इससे भी कम रखनी पड़ती है।

 

 

इन्सर्ट के बारे में ध्यान रखनेलायक एक और महत्वपूर्ण बात है, सरकन गति। आम तौर पर सरकन गति, इन्सर्ट की नाक की त्रिज्या की आधी (50%) होनी चाहिए। उदाहरण के लिए, अगर इन्सर्ट के नाक की त्रिज्या 0.8 मिमी. हो, तो हम 0.4 मिमी./परिभ्रमण से अधिक सरकन गति का इस्तेमाल नहीं कर सकते।

 

 

आजकल वाइपर इन्सर्ट की मांग हर दिन बढ़ती जा रही है। वाइपर बिंदु के कारण सरकन गति की सीमा पार करना संभव हो पाता है। नाक की त्रिज्या कम होने वाले इन्सर्ट को इस्तेमाल करते समय अगर काट की गहराई कम हो तो भी, ऐसे इन्सर्ट की मदद से अधिक सरकन गति पर यंत्रण करना संभव होता है। अधिकतम उत्पादकता चाहिए हो तो इस प्रकार के इन्सर्ट का इस्तेमाल सही साबित होता है।

सरकन गति बहुत कम भी नहीं होनी चाहिए क्योंकि अगर यह कम होगी तो कर्तन छोर यंत्रण ही नहीं कर पाएंगे और इन्सर्ट केवल कार्यवस्तु पर घिसता (रबिंग) रहेगा। F ज्यामिति के इन्सर्ट के इस्तेमाल से कम सरकन गति पर भी यंत्रण करना संभव होता है क्योंकि इस तरह के इन्सर्ट के कर्तन छोर, मुख्य रूप से कम सरकन गति के दृष्टिकोण से तैयार किए जाते हैं।

उचित आकार की चिप बनाने के लिए एक और महत्वपूर्ण घटक होता है, काट की गहराई और सरकन गति का अनुपात। यह उचित हो, तो बहुत लंबी या बहुत छोटी चिप का निर्माण नहीं होता। काट की गहराई और सरकन गति का अनुपात भी मर्यादा में होना चाहिए। लंबी चिप निकालने वाले मटीरीयल के मापन से यह पता चला है कि काट की गहराई और सरकन गति का अनुपात 5 से 15 के बीच होना चाहिए।

आम तौर पर काट की गहराई और सरकन गति का अनुपात 10 के करीब होना सबसे अच्छा समझा जाता है। उदाहरण के लिए, अगर हमने 0.3 मिमी./परिभ्रमण चुना हो, तो उसके लिए काट की गहराई 3 मिमी. होनी चाहिए।

 

 

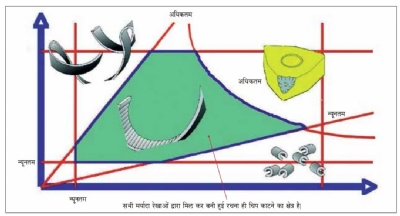
ऊपर दी गई सभी चर्चाओं का एकत्रित परामर्श हम चिप ब्रेकिंग की आकृति (चित्र क्र. 1) में से ले सकते हैं।

 

चित्र क्र. 1 चिप ब्रेकिंग आकृति

काट की गहराई ज्यादा भी नहीं और कम भी नहीं। सरकन गति भी, ज्यादा या कम नहीं। काट की गहराई और सरकन गति का अनुपात उतना ही होना चाहिए जितना चिप के उचित आकार के लिए आवश्यक हो। उसी प्रकार, काट की गहराई और सरकन गति का अनुपात अधिक नहीं होना चाहिए क्योंकि उसकी वजह से इन्सर्ट टूटने की संभावना ज्यादा होती है।

चिप हटाने का उचित मार्ग हमें चित्र क्र. 1 में साफ दिखाई देता है। अगर हम इस लेख में ऊपर दिए गए परिमाणों की मर्यादा के बाहर जा कर यंत्रण करेंगे तो समस्या जरूर आएगी।

 

 

टर्निंग प्रक्रिया में इन्सर्ट की ज्यामिति के परिमाण के बारे में बहुत कुछ कहा जा सकता है। कर्तन छोरों की ज्यामिति, कर्तन छोरों की ज्यामिति + चिप तोड़ने की ज्यामिति + इन्सर्ट के नाक की ज्यामिति का कुल योग होती है। इन तीनों ज्यामितीयों का उचित संयोजन कर के हम अधिक उचित तरीके से इन्सर्ट का चुनाव कर सकते हैं।

अगर इससे भी आगे जा कर ग्राहक को तकनीकी रूप से सर्वश्रेष्ठ इन्सर्ट चाहिए हो, तो नई MF5 ज्यामिति का विकल्प सबसे अच्छा होता है। इस तरह के इन्सर्ट के कर्तन बिंदु के पास स्थित MF ज्यामिति बेहद तेज (शार्प) होने के कारण कर्तन बल (कटिंग फोर्स) और उससे संबंधित अन्य पैरामीटर अल्प होते हैं।

 

 

इस तेज छोर का मिलाप, R प्रकार की ज्यामिति से होने के कारण काटने वाली तेज छोर, कर्तन छोर के एकदम पास यानि एक मिमी. के कुछ दशमलव हिस्से जितनी पास होती है। इस ज्यामिति के कारण चिप का आकार तैयार होने के लिए थोड़ी जगह दी जा सकती है, जिससे कर्तन छोर पर पड़ने वाला यंत्रण बल और भी कम हो जाता है।

इस संदर्भ से देखा जाए तो MF5 ज्यामिति यांत्रिक दृष्टि से अधिक मजबूत होती है और उसके कारण काट की गहराई और सरकन गति का चुनाव ज्यादा भरोसेमंद तरीके से किया जा सकता है। फलस्वरूप कर्तन बल और भी कम हो जाते हैं। टर्निंग प्रक्रिया में यह एक उपयोगी मुद्दा है क्योंकि इसके कारण हम कंपनों (वाइब्रेशन) का खतरा और भी घटा सकते हैं। उसी प्रकार इन्सर्ट द्वारा काम करवाने के लिए कम बल लगाना पड़ता है। साथ ही, कार्यवस्तु या कटिंग टूल मुड़ने का खतरा भी पैदा नहीं होता।

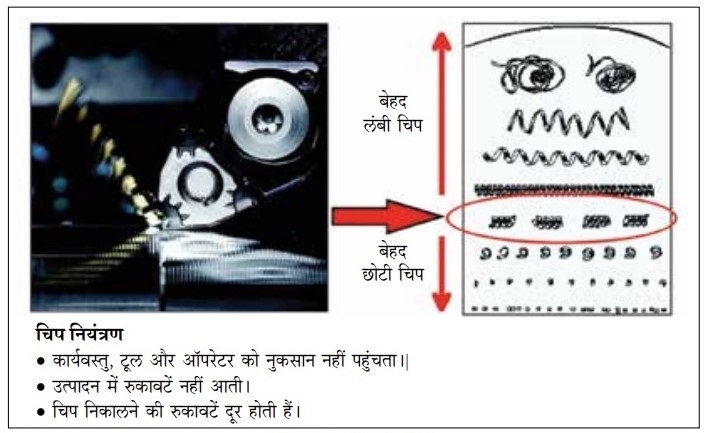
चित्र क्र. 2 : चिप नियंत्रण

 

इस प्रकार के इन्सर्ट का हम बारीकी से निरीक्षण करें, तो इन्सर्ट की नोक पर दो उभार दिखाई देते हैं, जो चिप का नियंत्रण (चित्र क्र. 2), कर्तन छोरों से दूरी पर करने में मदद करते हैं।

 

इन दो उभारों से हमें और भी अप्रत्यक्ष लाभ मिलते हैं। शीतक (कूलंट) के दबाव के साथ ही वे चिप को इन्सर्ट की नोक की तरफ धकेल कर एक तरह का दबाव कक्ष (चेंबर) निर्माण करते हैं। शीतक इस जगह में घुस कर, चिप की निचले हिस्से पर अधिक दबाव पैदा कर के चिप को ऊपरी दिशा में धकेलता है। इस दबाव के कारण चिप टूटने में मदद मिलती है। इस तरह की ज्यामिति हमें बहुत कम ही देखने को मिलती है। इससे यंत्रण किफायती होता है और ज्यादा लंबी चिप तैयार होने का खतरा पैदा नहीं होता।

 

MF5 ज्यामिति के इन्सर्ट का उचित इस्तेमाल करने से ऐसा कहा जा सकता है कि धातुकार्य के आधुनिक तरीके से किए जाने वाले काम के लिए इस ज्यामिति को खास तौर पर बनाया गया है।