अभियांत्रिकी ड्रॉइंगसंबंधि तरकीबें – 2
@@NEWS_SUBHEADLINE_BLOCK@@
Total Views |
पिछले लेख में हमने आरेखन की आवश्यकता तथा उसमें समय के अनुरूप होने वाले परिवर्तनों की जानकारी ली। साथ ही हमने आरेखन में इस्तेमाल होने वाले CAD साफ्टवेयरसंबंधि मूलभूत बातें समझ ली। इनमें हमने विभिन्न आदेशों (कमांड) का सटीक उपयोग, निर्बंधों (कन्स्ट्रेंट) के विभिन्न प्रकार तथा उनके इस्तेमाल की जानकारी, मिसालों के साथ ली।
इस लेख में हमने अत्यंत आधुनिक तकनीक 'पैरामैट्रिक ड्रॉइंग' के उपयोग से ड्रॉइंग को आसान और सुलभ कैसे किया जाए इसका विश्लेषण किया है।
कई जानीमानी कंपनियों के उत्पाद, मानकीकृत सूची (स्टैंडर्ड कैटलॉग) के अनुसार तैयार किए जाते हैं। उनके आयाम और उन्हें मापने की पद्धतियां भी पूर्वनिश्चित होती हैं। जैसे, 'O' रिंग, गैस्केट, फासनर आदि बनाने वाली कंपनियों के उत्पाद थोड़े फर्क से पुनरावृत्त होते रहते हैं। जैसे, कभी लंबाई बदलती है तो कभी व्यास किंतु अन्य घटक समान रहते हैं। तो कभी सभी माप समान होते हैं लेकिन कच्चा माल अलग रहता है। इसके लिए हर समय नया ड्रॉइंग बनाने की जरूरत होती है। इसमें जाने वाला समय किफायती नहीं होता। इसलिए रोजमर्रा के आरेखनों के लिए पैरामैट्रिक ड्रॉइंग संकल्पना प्रचलित हो रही है। पैरामैट्रिक ड्रॉइंग की मदद से नए आरेखन करने हेतु या पहले किए गए ड्रॉइंग में बदलाव करने के लिए इसका निश्चित तौर पर लाभ होता है। हम पहले पैरामैट्रिक ड्रॉइंग की एक मिसाल देखते हैं।
हमने ABCD यह आयत चुना तो उसका ड्रॉइंग बनाने हेतु उसकी लंबाई, चौड़ाई और मोटाई आदि जानकारी होना जरूरी है। प्रारूप तैयार करते समय उनके माप के सूत्र बना कर, पड़ताल कर के निश्चित किए जाते हैं। पैरामैट्रिक ड्रॉइंग में उस लंबाई का, चौड़ाई के साथ होने वाला अनुपात तय करना बेहद महत्वपूर्ण होता है। आप इसकी मिसाल आगे देख सकते हैं।
i. लंबाई X, चौड़ाई Y और मोटाई Z मानते हैं।
ii. लंबाई और चौड़ाई का अनुपात तय करते हैं।
Y = (X*0.6)
iii. लंबाई और मोटाई का भी अनुपात तय करते हैं।
Z = (X*0.25)
लंबाई = X = 40 मिमी.
Y = 40*0.6
चौड़ाई = Y = 24 मिमी.
Z = 40*0.25
मोटाई = Z = 10 मिमी.
इसे समझने के लिए चित्र क्र. 1 देखें।
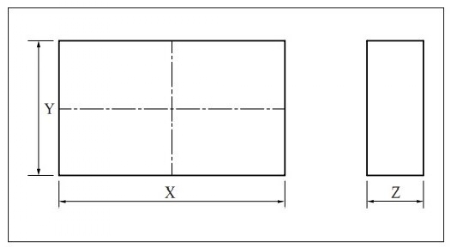
चित्र क्र. 1
उपरोक्त तीनों सूत्रों के अनुसार आयत की लंबाई, चौड़ाई और मोटाई निश्चित हुई है। इसके साथ वे एक दूसरे से संबंधित हुए हैं। अब लंबाई में परिवर्तन करने पर, उसकी चौड़ाई और मोटाई तय अनुपात के अनुसार अपनेआप बदलेगी। इस प्रकार, इस पद्धति की सिद्ध हुई उपयुक्तता आगे स्पष्ट की गई है।
• इन सभी परिवर्तनों के लिए कट, कॉपी, पेस्ट, डीलिट जैसे किसी भी कमांड के उपयोग को, नियोजित रूप से काम कर के टाला जा सकेगा।
• बहुत कम समय में यह परिवर्तन किए जा सकेंगे।
• गलतियां कम से कम होगी।
• ड्रॉइंग मानकीकरण करने की आदत बनेगी।
आयत की तरह वृत्त, चौकोन, त्रिकोण, षटकोन आदि कई आकार पैरामैट्रिक पद्धति से नियंत्रित किए जा सकते हैं।
जिस प्रकार हमने आयत जैसे विशिष्ट आकार का पैरामैट्रिक तरीके से आरेखन किया, वैसे ही पूरी वस्तु को पैरामैट्रिक पद्धति से तैयार किया जा सकता है। इसके लिए एक वस्तु की मिसाल का अध्ययन करेंगे।

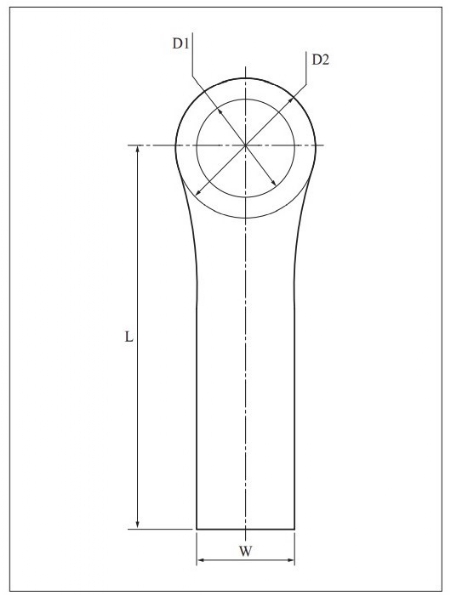
चित्र क्र. 2
चित्र क्र. 2 में विभिन्न प्रकार के आकार शामिल हैं। यहीं आकार, एक दूसरे के मापन पर निर्भर करने हेतु आयाम निश्चित करते हैं, जिससे एक आकार में बदलाव करने पर दूसरा आकार उसके तय अनुपात में बदलेगा। इसमें लंबाई 'L' से और चौड़ाई 'W' से दर्शाई है। चौड़ाई का लंबाई से अनुपात निश्चित करना जरूरी है। उसे अपने प्रारूप और गणन के अनुसार, अंत में तय कर सकते हैं। उसके लिए निश्चित सूत्र होना आवश्यक है, जैसे,
W = L/4 विधान i
मानिए कि L = लंबाई = 40 मिमी.
विधान i के अनुसार,
W = 40/4
चौड़ाई = W =10 मिमी.
इस सूत्र के अनुसार लंबाई और चौड़ाई, हमेशा के लिए एक दूसरे पर निर्भर हुई। इसी प्रकार पहले वृत्त के व्यास (D1) को दूसरे वृत्त के व्यास से जोड़ा जा सकता है, जिससे उन दोनों वृत्तों के बीच की दूरी अपेक्षित जितनी रहेगी और उनका अनुपात मानकीकृत होने में मदद मिलेगी। यह हम सूत्र के साथ स्पष्ट करते हैं।
D2 = 1.25*D1......... विधान i
सबसे पहले इसमें D1 यह मूलभूत व्यास है, क्योंकि इसमें वस्तु का अंतर्गत व्यास किसी अन्य वस्तु के व्यास से जुड़ने वाला है। इसलिए इस व्यास को निश्चित करना महत्वपूर्ण है। अब D1 को प्रधानता दे कर इसे निश्चित करते हैं।
मानिए D1 = 15 मिमी.
विधान i के अनुसार,
D2 = 1.25*15
= 18.75 मिमी.
बाहरी व्यास = D2 =18.75 मिमी.
इस प्रकार सूत्र तैयार कर के हम अब तक वस्तु की लंबाई, चौड़ाई, उनका अनुपात और अंतर्गत मूल वृत्त, बाह्य वृत्त का अनुपात, उसके अनुसार दो वृत्तों के बीच का अंतर निश्चित कर सके हैं। अब भविष्य में इसमें से कोई भी घटक, जैसे लंबाई, वृत्त के माप आदि में बदलाव हो तब उससे संबंधित अन्य मापों में अनुपात के अनुसार परिवर्तन होगा। हमें इसका बार बार गणन नहीं करना पड़ेगा, साथ में समय की भी बचत होगी।
यह संपूर्ण लेख पैरामैट्रिक ड्रॉइंग इस अत्याधुनिक पद्धति पर आधारित रहा है। हम इस पद्धति से आसान ड्रॉइंग का आरेखन तो कर सकते हैं लेकिन जटिल आरेखन के लिए यह पद्धति इतनी आसान नहीं होगी। क्योंकि अनुपात में बदलाव करने पर उसके परिणामों की व्याप्ति मर्यादा में रखना मुश्किल हो सकता है। लेकिन रोजमर्रा के आसान आरेखन करते समय इसका निश्चित रूप से लाभ होगा।
'स्टैंडर्ड टेम्प्लेट' कैसे तैयार करते हैं, वह तैयार करते समय किन घटकों का प्रमुखता से विचार करना आवश्यक है इसके बारे में अगले लेख में हम विस्तार से जानकारी लेंगे।
9823389389
अमित घोले यांत्रिकी अभियंता हैं। अैटलास कॉप्को, थिसेन क्रुप जैसी मल्टिनैशनल कंपनियों के डिजाइन विभाग में कई साल काम करने के बाद, आपने इंजीनीयरिंग डिजाइन सोल्यूशन और कॉर्पोरेट प्रशिक्षण देने वाली 'इमैजिका टेक्नोसाफ्ट' इस कन्सल्टन्सी की स्थापना की है।
@@AUTHORINFO_V1@@


