प्रयोगों का डिजाइन

 

 

1920 के दशक में कृषि उत्पादन में सुधार हेतु सर रोनाल्ड फिशर ने अथक प्रयास किए। श्रेष्ठ शास्त्रज्ञ फिशर, सांख्यिकी में एक जानामाना नाम है। उस समय 'ओफैट' (वन फैक्टर अैट अ टाइम) का बोलबाला था। कई घटकों पर निर्भर होने वाली किसी प्रक्रिया के संदर्भ में, एक समय पर एक ही घटक में बदलाव कर के होने वाले परिणामों को जांचा जाता है। इस तकनीक को ओफैट यह नाम है। फिशर ने, सांख्यिकी के उपयोग से अनेक चल घटक (वेरियेबल) होने वाली प्रक्रिया के बारे में अधिक जानकारी देने वाले प्रयोग डिजाइन किए।

 

 

हमें अगर उत्पादन और प्रक्रिया पर विभिन्न घटकों के होने वाले परिणाम का मूल्यमापन करना हो, तो सामान्यतः हम एक समय पर एक ही घटक में परिवर्तन कर के निरीक्षण को दर्ज करते हैं। जैसे, हमें कर्तन गति (कटिंग स्पीड) और सरकन गति (फीड) का इष्टतम सेटिंग करना हो, तो ओफैट की पारंपरिक पद्धति के अनुसार बेहतर पृष्ठीय फिनिश पाने के लिए पहले उचित कर्तन गति का पता लगाया जाएगा। उसके बाद, उस कर्तन गति पर सर्वोत्तम पृष्ठीय फिनिश देने वाली बेहतर सरकन गति का पता लगाया जाएगा। तथापि, भिन्न घटकों की एक दूसरे के साथ होने वाली आंतरक्रिया (इंटरैक्शन) को हम ओफैट में नहीं समझ सकते। आंतरक्रिया यानि एक घटक में किए गए परिवर्तन का, अन्य घटकों के सेटिंग पर पड़ने वाला प्रभाव। चूंकि ओफैट में इन आंतरक्रियाओं पर विचार नहीं किया जाता, इससे प्राप्त स्पीड और फीड के सर्वोत्तम सेटिंग वास्तव में इष्टतम होने का भरोसा नहीं दिया जा सकता। चित्र क्र. 1 देखें।

 

 

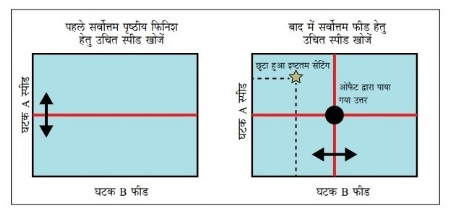
चित्र क्र. 1

 

इसलिए सांख्यिकी के इस्तेमाल से डिजाइन किए प्रयोगों की (स्टैटिस्टिकली डिजाइन्ड एक्सपेरीमेंट, SDE) सिफारिश, विशेषज्ञों द्वारा की जाती है। इसका लोकप्रिय नाम है डिजाइन ऑफ एक्सपेरीमेंट (DOE)। DOE का मुख्य लाभ है, कम परीक्षणों में अधिक ज्ञान मिलना!

 

इसमें प्रयोगों को LF कहा जाता है। इसमें F घटकों की संख्या हैं और L, हर घटक के स्तरों की संख्या है। जैसे, मानिए कि किसी प्रक्रिया के तीन घटक है और हर घटक के दो स्तर हैं। इसके लिए 23 अर्थात 8 प्रयोग करने होंगे। इसे एक पुनरावृति प्रयोग (रेप्लिकेट) कहते हैं।

 

इसी प्रकार प्रत्येक में 3 स्तर होने वाले 5 घटक हो, तो वह 35 प्रयोग होगा। उसके 3*3*3*3*3 अर्थात 243 परीक्षण होंगे। तालिका क्र. 1 में हम देख सकते हैं कि जैसे जैसे घटकों तथा स्तरों की संख्या बढ़ेगी, परीक्षणों की संख्या भी बढ़ती जाएगी।

 

परीक्षणों की संख्या ज्यादा न बढ़े, इसलिए अधिकतर प्रयोगों में प्रत्येक घटक के दो स्तरों पर ही विचार किया जाता है। अगर घटकों की संख्या 'K' होगी और हर एक के दो स्तर होंगे, तो हमें प्रयोग हेतु 2K परीक्षण करने होगे। यह प्रयोग की प्रतिकृति होगी। इस प्रयोग की अचूकता बढ़ाने के लिए पूरा प्रयोग दोहराना जरूरी होता है।

 

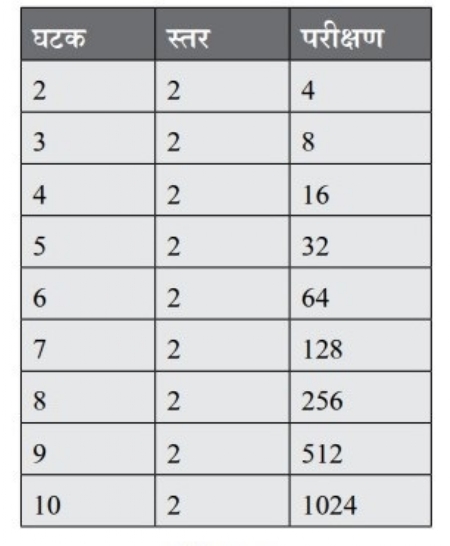
 तालिका क्र. 1

 

प्रयोगों के डिजाइन की संकल्पना मूलतः समझने हेतु हम, किसी यंत्रण प्रक्रिया में टूल की आयु बढ़ाने हेतु कर्तन के इष्टतम पैरामीटर खोजने के प्रयोग पर विचार करते हैं। यंत्रण प्रक्रिया में टूल की आयु को प्रभावित करने वाले, कर्तन गति (मीटर/मिनट) और रेक अैंगल इन दो ही घटकों का विचार करते हैं। धातु काटने की मूलभूत तकनीक और अपने अनुभव की मदद से इन दो घटकों के उपयोग की श्रेणी तय की जा सकती है। इस संदर्भ में, अपनी समझ के अनुसार जो घटक या उसका जो मूल्य अव्यवहार्य लगे उस पर समय गंवाने की आवश्यकता नहीं। इसी लिए अपने अनुभव के आधार पर हर घटक के दो 'स्तर' प्रयोग के लिए चुने जाते हैं। पैरामीटर की इस श्रेणी में संशोधन कर के, उससे प्राप्त परिणाम (यहाँ टूल की आयु) इष्टतम करने का हम प्रयास करने वाले हैं। हमने तालिका क्र. 2 में दिए हुए घटकों के उच्च एवं निम्न स्तर तय किए हैं। इन्हें घटकों के गुणधर्म भी कहा जाता है।

 

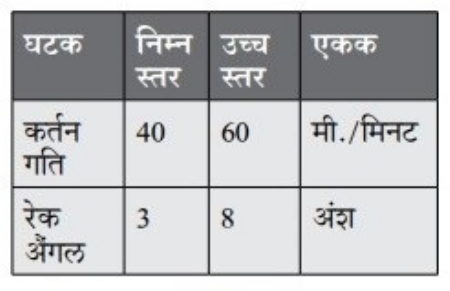
तालिका क्र. 2

 

अब हम इन घटकों एवं स्तरों के लिए एक मैट्रिक्स रचना तैयार करते हैं। इस रचना को 'फुल फैक्टोरियल डिजाइन' (FFD) कहा जाता है। FFD में हर घटक की हर स्तर पर जांच की जाती है। अर्थात इस प्रयोग में 2*2 = 4 परीक्षण किए जाएंगे।

 

पहले बताएनुसार, FFD में परीक्षणों की संख्या N = (स्तरघटक) होती है। प्रत्येक घटक, प्रत्येक अन्य घटक के हर स्तर पर जांचा जाने के कारण तालिका क्र. 3 के अनुसार प्रयोग किया जाएगा। प्रयोग द्वारा प्राप्त टूल की आयु की जानकारी, विश्लेषण हेतु इस तालिका में आपको उपलब्ध है। ये सारे परीक्षण स्वैर क्रम (रैंडम ऑर्डर) से करें, ताकि इस प्रयोग में शामिल न होने वाले अन्य घटकों का गंभीर प्रभाव अंतिम उत्तर पर न पड़े। यह चेतावनीयुक्त सुझाव, सांख्यशास्त्री हमे देते हैं।

 

अब देखते हैं कि प्रयोग द्वारा प्राप्त परिणामों का विश्लेषण कैसे करें। हर घटक का प्रभाव गिनने के लिए महत्वपूर्ण सूत्र आगे दिया है। यह सूत्र हर घटक के मुख्य प्रभावों तथा घटक की आंतरक्रियाओं को लागू होता है।

 

E = परिणाम

HR = उच्च स्तर पर औसत प्रतिक्रिया

LR = निम्न स्तर पर औसत प्रतिक्रिया

E = HR-LR

 

पहले हम रेक अैंगल के मुख्य प्रभाव की गणना करते हैं। तालिका क्र. 3 के अनुसार इसकी गणना बेहद आसान है।

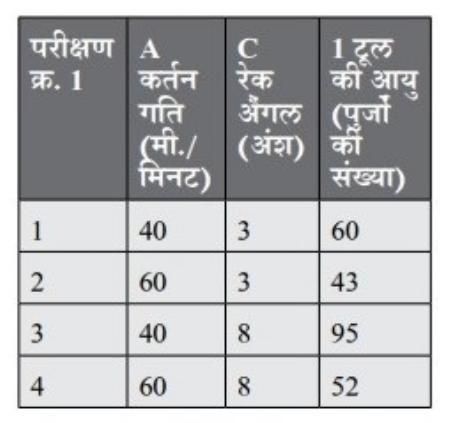
तालिका क्र. 3

 

रेक अैंगल के उच्च स्तर पर (8°), औसत मूल्य

(95+52)/2 = 73.5

इसी प्रकार, रेक अैंगल के निम्न स्तर पर (3°) औसत मूल्य

(60+43)/2 = 51.5

 

इसलिए हम निश्चित रूप से कह सकते हैं कि टूल की आयु पर रेक अैंगल का प्रभाव 73.5-51.5 =22 है। यह धन संख्या है, जिसका मतलब है जैसे रेक अैंगल 3° से 8° तक बढ़ता है, वैसे टूल की आयु में औसत 22 पुर्जों जितना सुधार होता है। आलेख क्र. 1 में दर्शाएनुसार उसका आलेख तैयार हो सकता है। इसको रेक अैंगल का मुख्य परिणाम आलेख भी कहा जाता है।

 

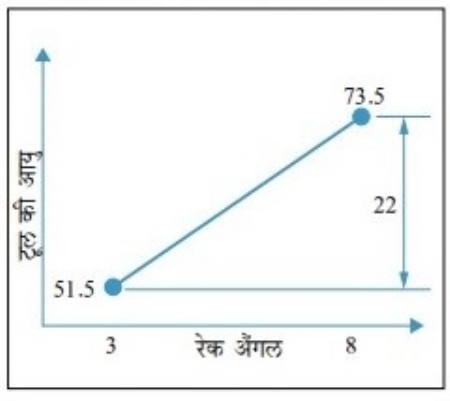
आलेख क्र. 1

 

इसी तरह अन्य घटकों के प्रभाव का गणन, आगे दिएनुसार किया जा सकता है।

 

· 60 कर्तन गति पर टूल की औसत आयु (43+52)/2=47.5

· 40 कर्तन गति पर टूल की औसत आयु (60+90)/2= 77.5

· इस प्रकार, कर्तन गति का प्रभाव (47.5-77.5)= -30

 

यहाँ घटाव के चिन्ह का अर्थ है, कर्तन गति 40 से 60 तक बढ़ाने पर टूल की आयु कम होती है। आलेख क्र. 2 में इसे दर्शाया गया है। यह कर्तन गति का मुख्य प्रभाव आलेख है।

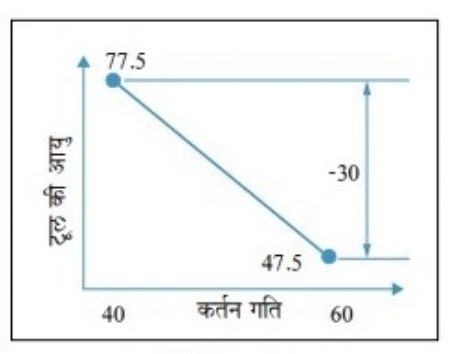
आलेख क्र. 2

 

इस प्रकार डिजाइन किए गए प्रयोगों में हम, सभी घटकों का सेटिंग एक ही समय बदल सकते हैं और फिर भी हर घटक का प्रभाव स्वतंत्र रूप से पा सकते हैं।

 

अब हम आंतरक्रिया के बारे में जानकारी लेते हैं। आंतरक्रिया अर्थात एक घटक का प्रभाव, अन्य घटक के सेटिंग पर निर्भर होना। जैसे, कर्तन गति का प्रभाव रेक अैंगल पर निर्भर हो सकता है, क्योंकि टूल की छोर पर बिल्टअप तैयार होना रेक के अैंगल पर निर्भर करता है या कर्तन बल में होने वाली कटौती पर। हमें अपने प्रयोगों पर आधारित आंतरक्रिया का अनुमान लेने हेतु, घटकों के स्तरों को संकेतन (कोड) द्वारा निर्देशित करना होगा। निम्न हेतु (-1) और उच्च हेतु (+1), यह संकेत हम निश्चित करेंगे। तो घटकों के स्तंभ के आंकड़ों का एक दूसरे से गुणाकार कर के हमें आंतरक्रिया स्तंभ में धन/ऋण चिन्हों समेत स्तर के आंकड़े मिलते हैं। इन आंतरक्रियाओं के लिए होने वाला AB यह अतिरिक्त स्तंभ, तालिका क्र. 4 में दर्शाया है।

 

आंतरक्रिया की गणना पहले जैसी ही है और इसमें उच्च (+) एवं निम्न (-) स्तर के फर्क दर्शाने वाले पहले सूत्र का ही उपयोग किया जाता है। इसलिए आंतरक्रिया आगे दिएनुसार होगी।

 

इस गणना के अनुसार, कर्तन गति और रेक अैंगल की आंतरक्रिया काफी बड़ी लगती है। इन घटकों के प्रमुख प्रभाव से भी वह अधिक है।

 

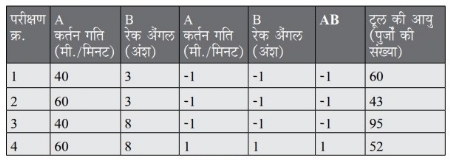
तालिका क्र. 4

 

इस प्रयोग में रेक अैंगल और कर्तन गति के बीच की आंतरक्रिया, आलेख क्र. 3 में दर्शाई है। समानांतर रेखाओं का मतलब, कोई भी आंतरक्रिया न होना ऐसा माना जाता है। उन रेखाओं में होने वाला कोण, उन घटकों की आंतरक्रिया के प्रभाव को दर्शाता है। कर्तन गति और रेक अैंगल की आंतरक्रिया का प्रभाव स्पष्ट रूप से दिखाई देता है।

 

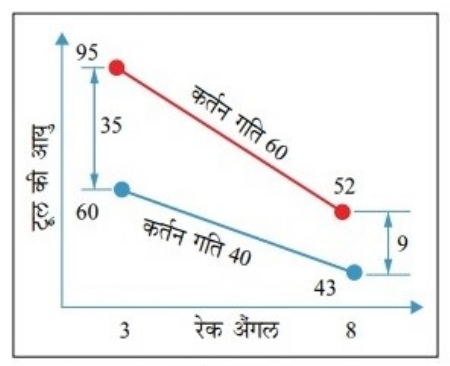
आलेख क्र. 3

 

आंतरक्रिया प्लॉट का आलेख में किया हुआ प्रस्तुतिकरण, प्रमुख प्रभाव से भिन्न प्रकार में किया गया है। एक घटक का प्रभाव, अन्य घटक के हर सेटिंग के लिए स्वतंत्र रूप से गिना गया है। जैसे, रेक अैंगल 3° पर सेट किया होने पर और बाद में रेक अैंगल बदल कर 8° पर सेट करने पर, कर्तन गति का प्रभाव गिना जाता है। इन दोनों प्रभावों के फर्क का आधा मूल्य, आंतरक्रिया का प्रभाव होता है। रेक अैंगल 3° होने पर, कर्तन गति 40 से 60 करने से मिलने वाला प्रभाव 35 है। यह आलेख क्र. 3 में दिखाया है। रेक अैंगल 8° होने पर, कर्तन गति 40 से 60 करने से मिलने वाला प्रभाव 9 है। इसका मतलब, रेक अैंगल 8° हो, तो कर्तन गति का प्रभाव रेक अैंगल 3° पर देखे गए प्रभाव से बेहद कम है। इन दोनों प्रभावों के फर्क का आधा हिस्सा (9-35)/2 = -26/2 = -13 है। इस प्रकार आंतरक्रिया का प्रभाव -13 है।

 

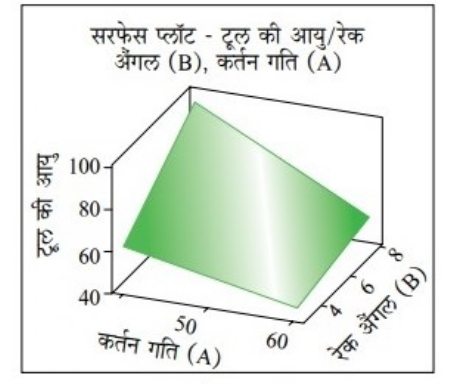
आलेख क्र. 4

 

हमारा अंतिम उद्देश्य है टूल की आयु अधिकतम करना। इसके लिए हम मिनिटैब जैसे साफ्टवेयर के इस्तेमाल से जटिल सांख्यिकी गणना कर सकते हैं। आलेख क्र. 4 में घटकों का सरफेस प्लॉट दर्शाया है। इस प्लॉट में वक्र भाग उल्लेखनीय है। इन दो घटकों की प्रभावी आंतरक्रिया के कारण यह हुआ है।

 

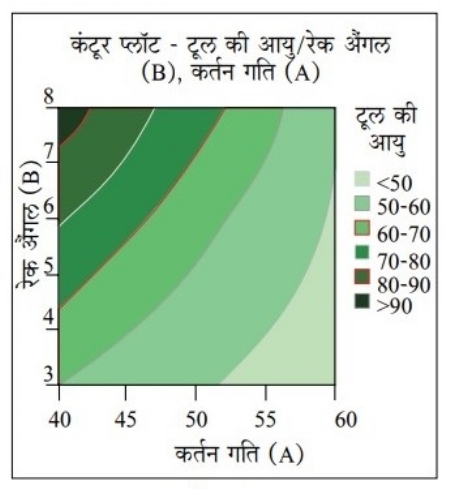
आलेख क्र. 5

 

आलेख क्र. 5 में दर्शाया कंटूर प्लॉट, घटकों का परस्पर प्रतिसाद देखने का एक और उपयोगी मार्ग है। अपेक्षा है कि इसमें सबसे गहरे रंग के जोन में टूल की सर्वाधिक आयु मिलेगी। साफ्टवेयर के ऑप्टिमाइजर के इस्तेमाल से, टूल की सर्वाधिक आयु देने वाली सेटिंग खोजना हमारा अंतिम उद्देश्य है। यहाँ स्पष्ट रूप से दिखता है कि कर्तन गति 40 और रेक अैंगल 8°, इस सेटिंग पर टूल की सर्वाधिक आयु मिलती है। जब घटकों की संख्या अधिक तथा आंतरक्रियाएं भी काफी होती हैं, ऐसे समय इष्टतम सेटिंग खोजना मुश्किल होता है। तब साफ्टवेयर फौरन जवाब देता है। कई बार एक से अधिक प्रतिक्रियाओं को इष्टतम करना होता है, जिसकी संकल्पना करना आसान नहीं होता। ऐसे वक्त साफ्टवेयर की मदद लेना उचित होता है।

 

सांख्यशास्त्रियों ने घटक तथा स्तर की संख्या के अनुसार प्रयोग करने हेतु, विशेष डिजाइन तैयार किए हैं। आम तौर पर, प्रयोगों के डिजाइन तथा विश्लेषण हेतु व्यावसायिक स्तर पर मिनिटैब जैसे साफ्टवेयर का उपयोग किया जाता है। जिससे सबसे उचित और स्थिर परिणाम प्राप्त होंगे, ऐसे घटकों के सेटिंग का अनुमान करने हेतु कई अतिरिक्त विशेषताएं इस साफ्टवेयर में उपलब्ध होती हैं।

 

घटकों की संख्या अधिक हो, तो अधिक संख्या में परीक्षण करने पड़ेंगे, यह एक स्वाभाविक सोच है। तथापि, बड़ी संख्या में घटक होने वाले प्रश्नों के उत्तर खोजने के लिए सांख्यशास्त्रियों ने फ्रैक्शनल फैक्टोरियल डिजाइन विकसित किया है। साफ्टवेयर के माध्यम से ये आसानी से इस्तेमाल किए जा सकते हैं।